Físicos criam o labirinto mais ‘diabolicamente’ difícil do mundo

Num artigo publicado recentemente na revista Physical Review X, três físicos britânicos descrevem como produziram o que chamaram “o labirinto mais terrivelmente difícil já criado”.

Combinando princípios da geometria fractal, com repetições infinitas de um padrão básico, e o antigo movimento do cavaleiro no jogo de xadrez, eles produziram os chamados ciclos hamiltonianos, descritos na teoria dos grafos como caminhos que visitam cada vértice uma vez e retornam ao vértice inicial, formando um ciclo fechado.

Este padrão, conhecido em revestimentos planos como ladrilhos Ammann-Beenker, forma intrincados labirintos fractais para representar quasicristais. Essas estruturas sólidas são comparadas pelos autores a uma forma exótica de matéria, devido às suas propriedades físicas e estruturais únicas que as diferenciam dos cristais tradicionais.

Labirintos construídos pelo “passeio a cavalo”

Representação de uma peça Ammann-Beenker. Fonte: Felix Flicker/Divulgação

A equipe utilizou um movimento banal, o deslocamento em “L” do cavalo em um jogo de xadrez, para construir um número infinito de ciclos newtonianos. Esses loops tornam-se cada vez maiores até descreverem matéria exótica chamada quasicristais. Esta forma, encontrada na natureza apenas em um meteorito na Sibéria, é cortada em cristais que vivem em seis dimensões.

Os fractais formados por quasicristais são descritos em um comunicado à imprensa como “um lápis apontado atomicamente“ traçar linhas retas ao redor de todos os átomos vizinhos, conectando-os sem tirar o instrumento do papel e sem sobrescrever as linhas.

Substituir o lápis por uma ponta de microscópio atomicamente afiada, que gera imagens de átomos individuais, esses ciclos hamiltonianos formariam as rotas mais fáceis para o dispositivo eletrônico. Isso seria de grande utilidade na pesquisa, pois o processo, conhecido como microscopia de varredura por tunelamento, pode levar até um mês para ser concluído.

Mais difícil que o Labirinto do Minotauro?

O labirinto mitológico da ilha de Creta foi projetado para que o Minotauro não pudesse escapar.Fonte: Imagens Getty

Para se ter uma ideia da complexidade dos labirintos desenvolvidos nesta pesquisa, vale faça uma comparação com o labirinto mítico do Minotauro, desenhado por Dédalo na mitologia grega. Esta armadilha, destinada a punir os jovens gregos, foi um desafio físico e mental, que também manteve o monstro preso.

Apesar de ser considerado intransponível, o labirinto do Minotauro era uma construção finita e concreta. Como tinha entrada e saída claras, o objetivo era encontrar uma maneira de escapar. Ou seja, apesar de complexo, não exigia ferramentas matemáticas avançadas.

Os labirintos de Ammann-Beenker são baseados em padrões quase periódicos, que demonstram complexidade matemática e estrutural avançada. Caracterizado por aperiodicidade e simetrias não convencionais, eles dependem da determinação de ciclos hamiltonianos para serem resolvidos matematicamente.

Possíveis aplicações práticas do labirinto intransponível

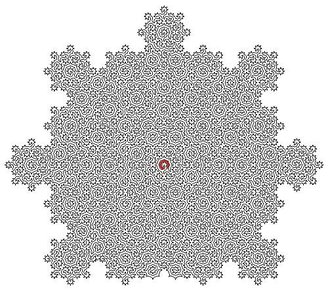Ciclo hamiltoniano completo.Fonte: Universidade de Bristol

Estas criações labirínticas únicas não visam apenas resolver problemas estéticos, mas têm utilizações potenciais em vários campos científicos e tecnológicos. Ao explorar a complexidade e as propriedades dos ciclos hamiltonianos, o estudo ajuda a resolver alguns problemas notoriamente difíceisdesde encontrar rotas mais rápidas para veículos até compreender o enovelamento de proteínas.

A pesquisa também demonstrou que os quasicristais podem ser transformados em adsorventes altamente funcionais. A adsorção, processo no qual as moléculas aderem à superfície de um sólido, pode ser usada para capturar carbono, evitando que o gás entre na atmosfera terrestre.

Em comunicado, o líder da pesquisa, Felix Flicker, da Universidade de Bristol, no Reino Unido, explica que a adsorção eficiente pode tornar os quasicristais catalisadores muito úteis para reduzir a energia das reações químicas e aumentar a eficiência industrial. “Nesse cenário, portanto, tornamos tratáveis ​​alguns problemas aparentemente impossíveis”, finaliza.

Você tem alguma pergunta? Conte para a gente em nossas redes sociais e entenda de uma vez por todas porque as ciências exatas são tão difíceis de aprender. Até tarde!